An Analogy to Dive Deep Into the Nature of Time

Time is a concept many philosophers and physicists pondered upon for centuries. It still remains mysterious besides the metaphysical claims of a few. Here, let us discuss an analogy that might serve in improving the understanding of how time works and draw parallels to the Eastern Philosophical thought which propounds certain properties to the fundamental nature of time.

Let us start with John Conway’s Game of Life, then discuss how a computer processor works and see an example of a similar approach in Theoretical Physics research. Finally, we get to ask deep questions while pondering on the axioms set out by Eastern Philosophers. We shall also take multiple detours to address some other related aspects.

Conway’s Game of Life #

We are starting with a complex system that is simple enough to study besides the fact that it has enough components for us to contemplate upon. John Conway, a famous mathematician(opinionated perhaps?), who worked on multifarious aspects of Math, developed a cellular automaton called Game of Life.

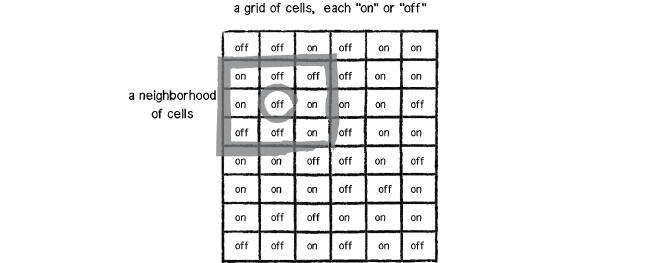
But first, what is a Cellular Automata? It is a model of a system with cell objects being its building blocks that follow some simple set of rules.

• These cells live on a grid.
• Each cell has a state. The number of state possibilities is typically finite. The simplest example has the two possibilities of 1 and 0.
• Each cell has a neighbourhood. This can be defined in any number of ways, but it is typically a list of adjacent cells.
• The cells in the grid interact and change their state according to some specific rules of the game. And the grid traverses the time in terms of generations by applying the rules to each cell present in the grid. Each generation represents the rules of the game applied to all the cells in the grid.

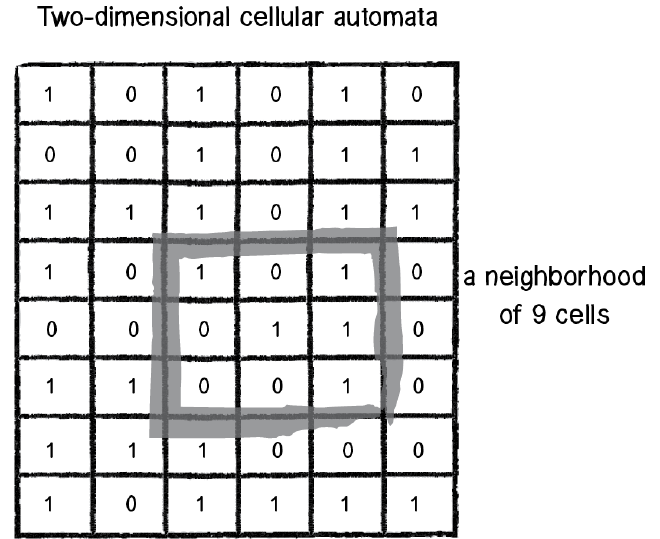
The development of cellular automata systems is typically attributed to Stanisław Ulam and John von Neumann, who were both researchers at the Los Alamos National Laboratory in New Mexico in the 1940s. Cellular Automata has its applications in a wide variety of fields, but let us keep ourselves to Game of Life which is a 2-D cellular automaton i.e, the grid is 2-D.

Rules of the Game: #

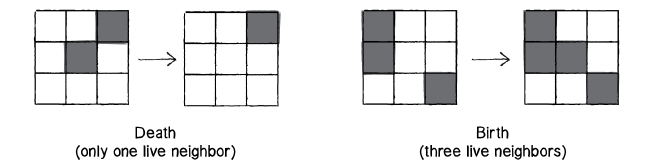
• Death. If a cell is alive (state = 1) it will die (state becomes 0) under the following circumstances. Overpopulation: If the cell has four or more alive neighbours, it dies.
• Loneliness: If the cell has one or fewer alive neighbours, it dies.
• Birth. If a cell is dead (state = 0) it will come to life (state becomes 1) if it has exactly three alive neighbours (no more, no less).
• Stasis. In all other cases, the cell state does not change. To be thorough, let’s describe those scenarios. Staying Alive: If a cell is alive and has exactly two or three live neighbours, it stays alive.
• Staying Dead: If a cell is dead and has anything other than three live neighbours, it stays dead. Let’s have a look at a few examples as shown below:

Experiment Time #

Here is a simple playground to experiment with the Game of Life.

• The input option will take input from us for an initial state of the cells in the grid.
• The simulate option helps to traverse the generation using the game rules.
• The Random option generates an initial state using pseudo-random number generators and starts the simulation for us automatically.
• The Reset option helps to clean the slate for us to start afresh simulation.
• The slider in the top left corner helps you to speed up or slow down the simulation runtime. The extreme left will display a generation for a second before switching to the newer generation, the extreme right will switch 255 generations in a second, so feel free to adjust the slider for your comfort.

IF something appears broken, clicking it again might make it work. This is a run-of-the-mill program (with no optimizations) written using the p5.js Javascript library for a quick reference.

Here is the source code if you are interested in modifying it or changing the world size to a bigger one. To change the world size, just change the parameters of the createCanvas(854, 480); function at the top of the file. As you can see, the current simulation is running in 480p resolution but has approximately 4100 cells. Increasing the resolution will increase the cell number which you have to do with caution as your CPU might be overloaded and you might experience a browser crash.

Observations #

Now, let us look at some undiscussed basis upon which this cellular automaton works. Time is represented as the counting of generations and our loops implement the laws of the world on every iteration. Hence, time is mapped as a counting function here.

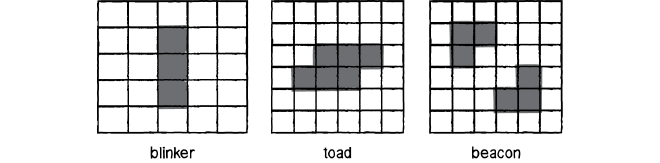
Another observation is, we have some emergent phenomena from the seemingly simple rules of this world. We have static, oscillator, movement and generator figures popping up based on these simple laws of the world. Have a look at the below image:

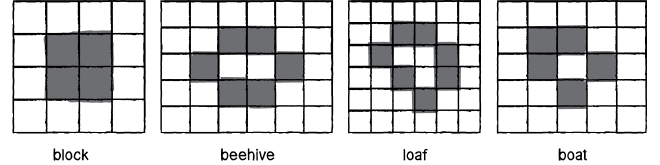
The above image represents possible shapes that stay the same as generations progress (or time progresses).

The above image shows us the oscillatory shapes with different periods. This page shows more collections. How fascinating that a periodic structure should emerge from such simple concepts!

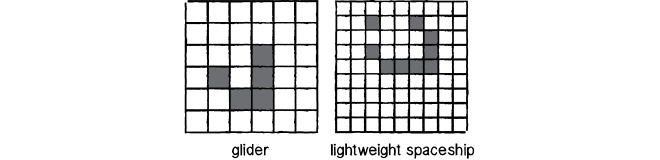
The above image patterns make a movement w.r.t every generational increment. Actually, nothing is moving according to automata but it appears to be moving from the top view; we could call it an abstraction.

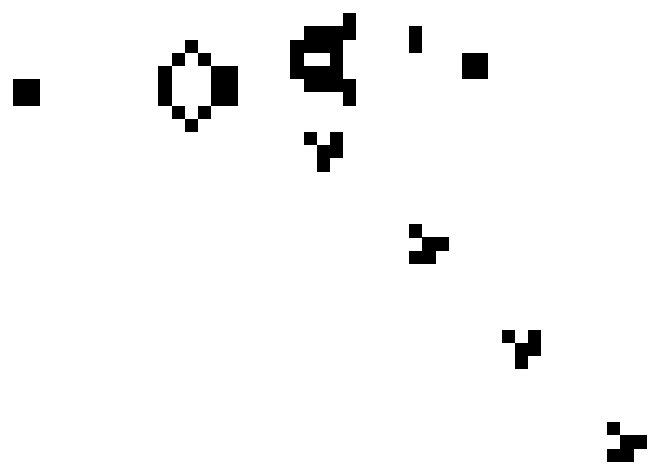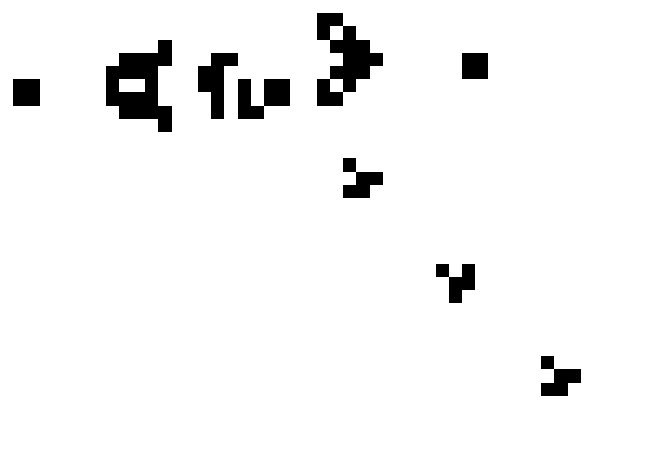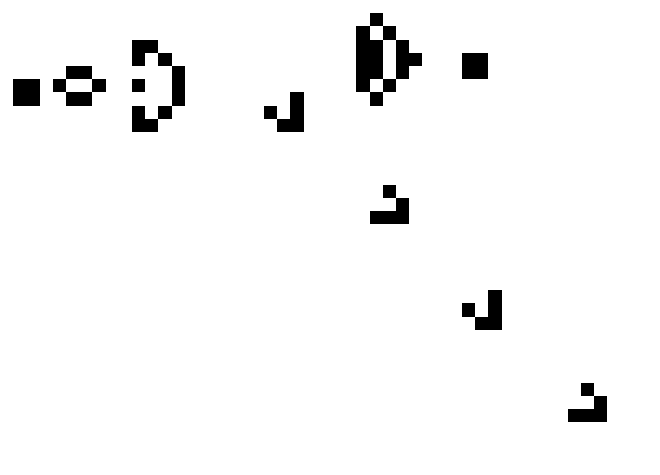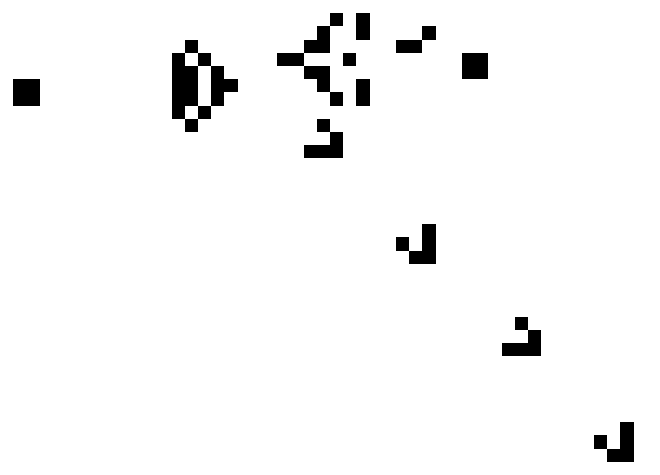
The above shape constantly generates new moving entities in our cellular automata.

Where are we going with these observations? We see an atmosphere where living, death, migration, reproduction and other complex mechanisms become emergent from simple rules of a checkerboard world which doesn’t discuss such things in the first place.

Another observation is, the laws and the space is given to this world. They constitute the world and their interaction emerge more phenomena. The word interaction here is the key, we will get back to this point in the later section of this article.

This discussion can also lead to Turing machines and their related interesting phenomena, more on that in a future article.

CPU’s Amazing Construction #

I will boldly state that the CPU of a computer is one of the best technological innovations and marvels Humans have ever achieved. It has a lot of management and architectural principles in it which can teach us a lesson or two. Let us jump right to the section which matters the most to us, time.

How do computers manage to keep track of time? IF we run a program in a computer, such as the above for example, we see that the loop’s iteration is mimicking the time in the simulated world. If we dig deeper, the CPU executes a certain number of instructions per second. How? Here is how it does so.

If you have studied basic electronic circuits and boolean algebra, you should recognize the below diagram with little difficulty.

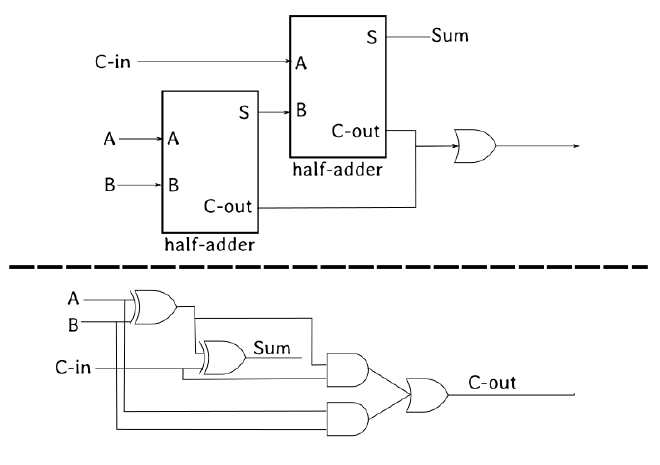
It is a full adder circuit. What does it do? It adds two numbers. How does it do? We send voltage signals into it and the logical gates will process those signals using simple boolean arithmetic and give out some voltage signals which we have to parse back to human-readable format. Now, look at the circuit below:

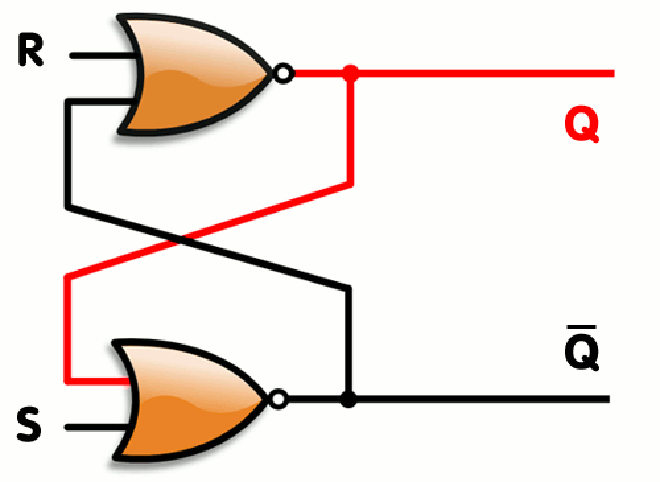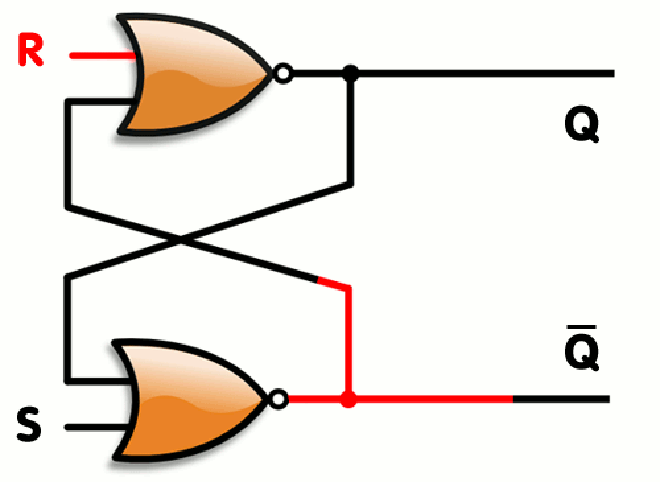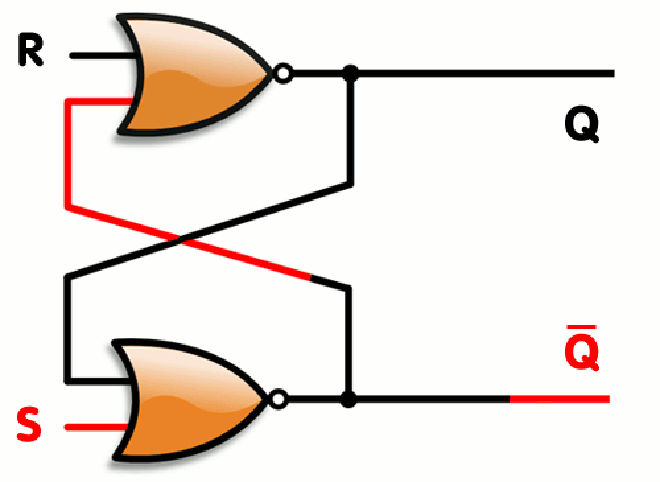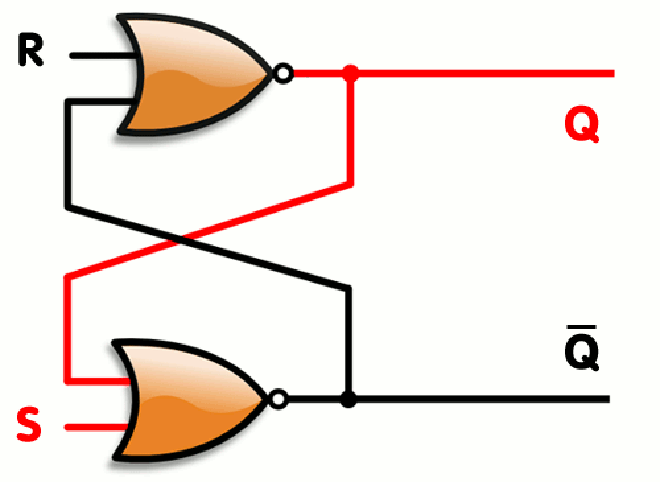
This one is called a flip-flop, it is used to store data persistently. Why am I saying all this instead of discussing time? Here is why; a CPU is basically a huge collection of these circuits, fabricated using VLSI design(basically creating a circuit in micro/nanometer scales on a silicon wafer), which works as the signals are being sent.

Here is the rub, the signals sent happen based on the time which is kept track in the computer. How is it kept track of, you ask? There is something called an RTC(Real Time Clock) which is connected to a Quartz crystal that oscillates at a certain frequency. The engineering of how they modify that frequency involves piezo-electricity and some analog electronics which we will not look into here. But, the fact is, the Oscillations of Quartz crystal is counted and the time is interpreted based on that. If not Quartz crystal, we can have an LC circuit with a capacitor charged before being connected to the inductor to simulate such an oscillation or we have more complex analog circuits to generate oscillations(like using IC 741 OP-AMP for example) but let us not worry about it here.

IF the oscillation frequency of the installed Quartz crystal is 100 MHz, then if we count 10^8 oscillations of the crystal using a counter circuit, we know 1 second has passed. Simple enough right? Did you notice what happens here? We count to represent time.

The circuits above will run only if this counting is kept intact, i.e, time is a necessary ingredient for the functioning of the CPU. The code can be highly complex, but it needs time to set it in motion, just like Hamiltonian which generates the flow of time in physical systems!

General Remarks and Branching Detours #

Comparing Conway’s Game of Life and CPU’s construction, we see counting leads to the representation of time. If we are to simulate a complex system which might accommodate a sentient being, how will it perceive the time moving in his world? How will he perceive the fact that it is us who pushed the start button for the simulation? He may conduct millions of scientific experimentation only to discover the immediate causes. How will he discover the efficient cause (which is us) using the scientific method?

What is a periodic structure? Something repeating w.r.t a linear structure. For example, we count Quartz crystal oscillations to measure time, a periodic entity w.r.t a linear structure which is the natural number system. If we unwrap the periodic structure, will the linear structure be still linear? Or will it turn periodic?

For example, consider one of the foci(or any other point in the place which we are about to discuss for the matter) of an ellipse. Let us say that a cart is traversing on the ellipse. We can represent the position of the cart w.r.t time using a parametric relation. What happens if we observe the point from the cart? The cart seems to be the focus of an elliptical path which this point we marked up moves in this system. A simple coordinate transformation and parametric elimination would show what I claim: if you require proof.

Let us do the same math but with a straight line and a tangent function. What happens? We first face the domain-range incompatibility problem, but we can mitigate such problems by considering modulo 2π. Here we see the linear structure becomes periodic and the periodic structure becomes linear!

Will the same scenario result in the case of unwrapping any periodic w.r.t to a linear structure? Is the bifurcation of the idea of the periodic and linear structure an illusion? Why I ask this is because if you have been in a Real Analysis 101 class, you will know all about the difficulty of defining a rigorous definition for the cardinality of a set. The definition seems circular or recursive.

For the sake of keeping this article small enough, I have attached a file that lists all the mathematical calculations which support the statements stated in the above few paragraphs.

Energetic Causal Sets #

Dr Lee Smolin of Perimeter Institue has started this topic of Energetic Causal Sets. This is very similar to Conway’s Game of Life except that this tries to simulate a real-world based on a graph data structure(instead of a grid/array) which represents causality between events. Prof Lee has taken this causal structure, energy-momentum and event as fundamental quantities of his theory and guess what? The theory shows the emergence of space, Bohmian Mechanics(Quantum Mechanics with some flavour of determinism with the help of hidden variables), configuration space, geometry, gauge fields and a few more. More details on this theory are beyond this article’s scope to discuss.

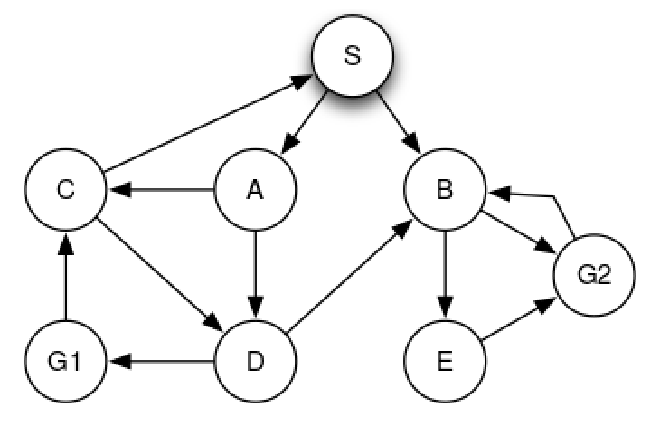
Apart from all the wonderful features of this model, one important aspect here is the nature of time. Time is taken to be constructive/present before the space and other theories emerge. In simple terms, time is a fundamental quantity and a necessary ingredient for the emergence of the universe. While philosophers like McTaggart propound that time is an illusion(more on that here and the world exists without time, Prof Lee is taking the other route. I wish to look into this formalism in more detail in the near future. If you wish to know more about his formalism, you can watch a video by Prof Lee where he presents this formalism in an International Conference called “Quantizing Time” (of which I was also a participant) here.

Eastern Philosophy #

Time is said to be unmanifested energy. It is the element that sets in motion the interaction between different material elements. The measure of time is two-fold, one the atomic time and the other the great time; the atomic time is the time taken by the sun to traverse a distance of atoms and the great time is the time taken to cover the entire existence of the nondual manifestation. Here too, the measure of time is counted based on some reference.

The influence of time brings the difference between manifest and unmanifest realities(similar to the “events” in Prof Lee’s work) and the entities which exist beyond its influence has nothing unmanifest. Time also has the function of dissociating the interactions it sets forth. There are many more peculiar details about the nature of time in the texts but we shall stop here.

The Resolution #

We have already looked at some questions like the similitude of linear and periodic structures, time as counting, generation of the flow of time and a lot more. We shall address a few more here to feed food for our thoughts.

Consider the situation of sentient beings in the simulation again. How will they understand the immediate cause of us starting the simulation of their world? How will they distinguish between immediate and efficient causes? How will they see the origin of their Universe? How does counting oscillations of crystals map to the movement of time(perhaps, it is to do with the discretization of continuous phenomena?)? How do we test if we are running in a simulation(Nick Bostrom’s Idea?)? This study of time also brings forth the distinction of the nature of the sentient beings in the simulation, can there be matter and spirit or is it all matter? What could be the interfacing elements between matter and spirit?

Should we really conclude the fact that McTaggart was right to claim that time is an illusion? Or we push forward and deal with the “unmanifest” nature of time. Time being unmanifest makes all this illusion and counting troubles is my take on it. But we represent time as counting which we perfected for our use cases; a construct, but does it make an impact on the nature of the world or the nature of nature of the model(meta-nature of the model) under the study?

Answers to these questions will come from a more deep research in this direction regarding the nature of time.

References: #

• The Nature of Code
• Conway’s Game of Life - Wikipedia
• Smolin, L. (2021). The emergence of quantum mechanics and space, from a fundamental, active time. Perimeter Institute. https://pirsa.org/21060098
• Srimad Bhagavatam 3rd and 11th Canto